Python

What is python

Python is an interpreted, object-oriented, high-level programming language with dynamic semantics. […]

It is suitable for rapid development and for use as a “glue language” to connect various components (e.g., written in different languages).

Python is one of the most used programming languages[1]

[1]: StackOverflow’s 2021 survey

Why is python so popular?

Its popularity can be rooted to its characteristics

Python is fast to learn, very versatile and flexible
It is very high-level, and complex operations can be performed with few lines of code

And to its large user-base:

Vast assortment of libraries
Solutions to your problems may be already available (e.g., on StackOverflow)

Some real-world applications

Data science (loading, processing and plotting of data)
Scientific and Numeric computing
Modeling and Simulation
Web development
Artificial Intelligence and Machine Learning
Image and Text processing
Scripting

How to get python?

Using the default environment that comes with your OS is not a great idea:

Usually older python versions are shipped
You cannot upgrade the python version or the libraries freely
Some functions of your OS may depend on it

You can either:

Download python
Use a distribution like Anaconda

Anaconda

Anaconda is a python distribution that packs the most used libraries for data analysis, processing and visualization

Anaconda installations are managed through the conda package manager

Anaconda “distribution” is free and open source

Anaconda distribution

Python virtual environments

A virtual environment is a Python environment such that the Python interpreter, libraries and scripts installed into it are isolated from those installed in other virtual environments

Environments are used to freeze specific interpreter and libraries versions for your projects

If you start a new project and need newer libraries, just create a new environment

You won’t have to worry about breaking the other projects

Environment creation

conda create –name <ENV_NAME> [<PACKAGES_LIST>] [–channel ]

You can also specify additional channels to search for packages (in order)

Example:

conda create –name gt python=3.9 graph-tool pytorch torchvision torchaudio cudatoolkit=11.3 pyg seaborn numpy scipy matplotlib jupyter -c pyg -c pytorch -c nvidia -c anaconda -c conda-forge

Switch environment

conda activate <ENV_NAME>

Example

conda activate gt

Full documentation

Data analysis and visualization libraries

NumPy
SciPy
Matplotlib
Seaborn
Pandas

These libraries are general, and can be used also in Network Analysis

Network analysis and visualization libraries

graph-tool
PyTorch Geometric (PyG)

NumPy

NumPy is the fundamental package for scientific computing in Python.

NumPy offers new data structures:

Multidimensional array objects (the ndarray)
Various derived objects (like masked arrays)

And also a vast assortment of functions:

Mathematical functions (arithmetic, trigonometric, hyperbolic, rounding, …)
Sorting, searching, and counting
Operations on Sets
Input and output
Fast Fourier Transform
Complex numbers handing
(pseudo) random number generation

NumPy is fast:

Its core is written in C/C++
Arrays are stored in contiguous memory locations

It also offers tools for integrating C/C++ code

Many libraries are built on top of NumPy’s arrays and functions.

The ndarray

Mono-dimensional	Multi-dimensional

NumPy documentation

import numpy as np

np.random.rand(3)

array([0.23949294, 0.49364534, 0.10055484])

np.random.rand(1, 3)

array([[0.45292492, 0.32975629, 0.53797728]])

np.random.randint(10, size=(2, 2, 2))

array([[[9, 1],
        [9, 9]],

       [[5, 7],
        [3, 3]]])

SciPy

SciPy is a collection of mathematical algorithms and convenience functions built on the NumPy library

SciPy is written in C and Fortran, and provides:

Algorithms for optimization, integration, interpolation, eigenvalue problems, algebraic equations, differential equations, statistics, etc.
Specialized data structures, such as sparse matrices and k-dimensional trees
Tools for the interactive Python sessions

SciPy’s main subpackages include:

Data clustering algorithms
Physical and mathematical constants
Fast Fourier Transform routines
Integration and ordinary differential equation solvers
Linear algebra
…
…
N-dimensional image processing
Optimization and root-finding routines
Signal processing
Sparse matrices and associated routines
Spatial data structures and algorithms
Statistical distributions and functions

import scipy as sp

SciPy documentation

Sparse matrices

There are many sparse matrices implementations, each optimized for different operations.

For instance:

Coordinate (COO)
Linked List Matrix (LIL)
Compressed Sparse Row (CSR)
Compressed Sparse Column (CSC)

Check this nice tutorial for more! Sparse matrices tutorial

Pandas

pandas allows easy data organization, filtering, analysis and plotting

pandas provides data structures for “relational” or “labeled” data, for instance:

Tabular data with heterogeneously-typed columns, as in an Excel spreadsheet
Ordered and unordered time series data
Arbitrary matrix data (even heterogeneous typed) with row and column labels

The two primary data structures provided are the:

Series (1-dimensional)
DataFrame (2-dimensional)

Series	DataFrame

These structures heavily rely on NumPy and its arrays

pandas integrates well with other libraries built on top of NumPy

Supported file formas

pandas can recover data from/store data to SQL databases, Excel, CSVs…

import pandas as pd

pandas documentation

DataFrame example

Penguins example dataset from the Seaborn package

penguins = sns.load_dataset("penguins")
display(penguins)

	species	island	bill_length_mm	bill_depth_mm	flipper_length_mm	body_mass_g	sex
0	Adelie	Torgersen	39.1	18.7	181.0	3750.0	Male
1	Adelie	Torgersen	39.5	17.4	186.0	3800.0	Female
2	Adelie	Torgersen	40.3	18.0	195.0	3250.0	Female
3	Adelie	Torgersen	NaN	NaN	NaN	NaN	NaN
4	Adelie	Torgersen	36.7	19.3	193.0	3450.0	Female
...	...	...	...	...	...	...	...
339	Gentoo	Biscoe	NaN	NaN	NaN	NaN	NaN
340	Gentoo	Biscoe	46.8	14.3	215.0	4850.0	Female
341	Gentoo	Biscoe	50.4	15.7	222.0	5750.0	Male
342	Gentoo	Biscoe	45.2	14.8	212.0	5200.0	Female
343	Gentoo	Biscoe	49.9	16.1	213.0	5400.0	Male

344 rows × 7 columns

Series of the species

penguins["species"]

0      Adelie
1      Adelie
2      Adelie
3      Adelie
4      Adelie
        ...  
339    Gentoo
340    Gentoo
341    Gentoo
342    Gentoo
343    Gentoo
Name: species, Length: 344, dtype: object

Unique species

penguins["species"].unique()

array(['Adelie', 'Chinstrap', 'Gentoo'], dtype=object)

Average bill length

penguins["bill_length_mm"].mean()

43.9219298245614

Standard deviation of the bill length

penguins["bill_length_mm"].std()

5.4595837139265315

Data filtering for male penguins

penguins["sex"] == "Male"

0       True
1      False
2      False
3      False
4      False
       ...  
339    False
340    False
341     True
342    False
343     True
Name: sex, Length: 344, dtype: bool

penguins.loc[                         # .loc property
    penguins["sex"] == "Male"         # Row filter (boolean)
]

	species	island	bill_length_mm	bill_depth_mm	flipper_length_mm	body_mass_g	sex
0	Adelie	Torgersen	39.1	18.7	181.0	3750.0	Male
5	Adelie	Torgersen	39.3	20.6	190.0	3650.0	Male
7	Adelie	Torgersen	39.2	19.6	195.0	4675.0	Male
13	Adelie	Torgersen	38.6	21.2	191.0	3800.0	Male
14	Adelie	Torgersen	34.6	21.1	198.0	4400.0	Male
...	...	...	...	...	...	...	...
333	Gentoo	Biscoe	51.5	16.3	230.0	5500.0	Male
335	Gentoo	Biscoe	55.1	16.0	230.0	5850.0	Male
337	Gentoo	Biscoe	48.8	16.2	222.0	6000.0	Male
341	Gentoo	Biscoe	50.4	15.7	222.0	5750.0	Male
343	Gentoo	Biscoe	49.9	16.1	213.0	5400.0	Male

168 rows × 7 columns

Average bill length for male penguins

penguins.loc[ penguins["sex"] == "Male",   # Mask (row filter)
              "bill_length_mm",            # Column filter
].mean()

45.85476190476191

Average bill length and weight for female penguins

penguins.loc[penguins["sex"] == "Female",                # Mask (row filter)
             ["bill_length_mm", "body_mass_g"]           # Column filter
            ].mean()

bill_length_mm      42.096970
body_mass_g       3862.272727
dtype: float64

Matplotlib

Matplotlib is a comprehensive library for creating static, animated, and interactive visualizations in Python

Matplotlib documentation

Barplots

Simple barplot

Source

Stacked barplot

Source

Grouped barplot

Source

Horizontal bar chart

Source

(Nested) pie charts

Source

Heatmaps

Source

Violin and box plots

Source

Stackplots

Source

… and many more

import matplotlib.pyplot as plt

Seaborn

Seaborn is a library for making statistical graphics in Python

Thanks to its high-level interface, it makes plotting very complex figures easy

Seaborn builds on top of matplotlib and integrates closely with pandas data structures

import seaborn as sns

It provides helpers to improve how all matplotlib plots look:

Theme and style
Colors (even colorblind palettes)
Scaling, to quickly switch between presentation contexts (e.g., plot, poster and talk)

sns.reset_defaults()

plt.plot(range(10), range(10))

[<matplotlib.lines.Line2D at 0x7f1ed75972b0>]

sns.set_theme(context="talk",
              style="ticks",
              palette="deep",
              font="sans-serif",
#               font_scale=1,
              color_codes=True,
              rc={
                  'figure.facecolor': 'white'
#                   'figure.figsize': (10, 6),
#                   "text.usetex": True,
#                   "font.family": "sans-serif",
              },
            
              )

plt.plot(range(10), range(10))
sns.despine()

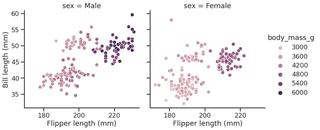
Seaborn’s FacetGrid offers a convenient way to visualize multiple plots in grids

They can be drawn with up to three dimensions: rows, columns and hue

Tutorial: Building structured multi-plot grids

penguins.head()

	species	island	bill_length_mm	bill_depth_mm	flipper_length_mm	body_mass_g	sex
0	Adelie	Torgersen	39.1	18.7	181.0	3750.0	Male
1	Adelie	Torgersen	39.5	17.4	186.0	3800.0	Female
2	Adelie	Torgersen	40.3	18.0	195.0	3250.0	Female
3	Adelie	Torgersen	NaN	NaN	NaN	NaN	NaN
4	Adelie	Torgersen	36.7	19.3	193.0	3450.0	Female

g = sns.relplot(data=penguins,
                x="flipper_length_mm",
                y="bill_length_mm",
                col="sex",
                hue="body_mass_g"
               )
g.set_axis_labels("Flipper length (mm)", "Bill length (mm)")

<seaborn.axisgrid.FacetGrid at 0x7f1ed7597a90>

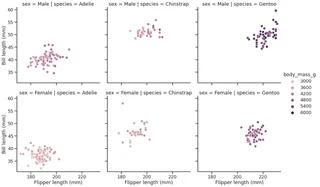
g = sns.relplot(data=penguins,
                x="flipper_length_mm",
                y="bill_length_mm",
                row="sex",
                col="species",
                hue="body_mass_g"
               )
g.set_axis_labels("Flipper length (mm)", "Bill length (mm)")

<seaborn.axisgrid.FacetGrid at 0x7f1ed73a5f10>

Seaborn documentation

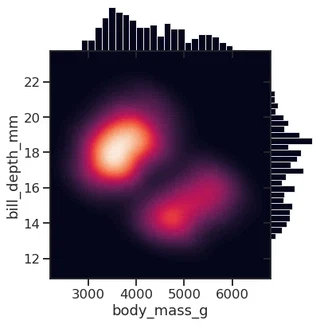
Some more plot examples

From Seaborn example gallery

Smooth kernel density with marginal histograms (source)

g = sns.JointGrid(data=penguins, x="body_mass_g", y="bill_depth_mm", space=0)
g.plot_joint(sns.kdeplot,
             fill=True, clip=((2200, 6800), (10, 25)),
             thresh=0, levels=100, cmap="rocket")
g.plot_marginals(sns.histplot, color="#03051A", alpha=1, bins=25)

<seaborn.axisgrid.JointGrid at 0x7f1ed5671ca0>

Joint and marginal histograms

Source

g = sns.JointGrid(data=planets, x="year", y="distance", marginal_ticks=True)

# Set a log scaling on the y axis
g.ax_joint.set(yscale="log")

# Create an inset legend for the histogram colorbar
cax = g.figure.add_axes([.15, .55, .02, .2])

# Add the joint and marginal histogram plots
g.plot_joint(
    sns.histplot, discrete=(True, False),
    cmap="light:#03012d", pmax=.8, cbar=True, cbar_ax=cax
)
g.plot_marginals(sns.histplot, element="step", color="#03012d")

<seaborn.axisgrid.JointGrid at 0x7f1ed4503c70>

Custom projections

Source

Discovering structure in heatmap data

Source

Bivariate plot with multiple elements

Source

Network Analysis with Python

Three main libraries:

graph-tool
networkx
python-igraph

graph-tool

graph-tool is a graph analysis library for Python

It provides the Graph data structure, and various algorithms

It is mostly written in C++, and based on the Boost Graph Library

It supports multithreading and it is fairly easy to extend

Built in algorithms:

Topology analysis tools
Centrality-related algorithms
Clustering coefficient (transitivity) algorithms
Correlation algorithms, like the assortativity
Dynamical processes (e.g., SIR, SIS, …)
Graph drawing tools
Random graph generation
Statistical inference of generative network models
Spectral properties computation

Documentation

import graph_tool.all as gt

Performance comparison (source: graph-tool.skewed.de/)

Algorithm	graph-tool (16 threads)	graph-tool (1 thread)	igraph	NetworkX
Single-source shortest path	0.0023 s	0.0022 s	0.0092 s	0.25 s
Global clustering	0.011 s	0.025 s	0.027 s	7.94 s
PageRank	0.0052 s	0.022 s	0.072 s	1.54 s
K-core	0.0033 s	0.0036 s	0.0098 s	0.72 s
Minimum spanning tree	0.0073 s	0.0072 s	0.026 s	0.64 s
Betweenness	102 s (~1.7 mins)	331 s (~5.5 mins)	198 s (vertex) + 439 s (edge) (~ 10.6 mins)	10297 s (vertex) 13913 s (edge) (~6.7 hours)

How to load a network

Choose a graph analysis library. The right one mostly depends on your needs (e.g., functions, performance, etc.)
In this warm-up, we will use graph-tool.
To load the network, we need to use the right loader function, which depends on the file format

File formats

Many ways to represent and store graphs.

The most popular ones are:

edgelist
GraphML

For more about file types, check the NetworkX documentation

Edgelist (.el, .edge, …)

As the name suggests, it is a list of node pairs (source, target) and edge properties (if any). Edgelists cannot store any information about the nodes, or about the graph (not even about the directedness)

Values may be separated by commas, spaces, tabs, etc. Comments may be supported by the reader function.

Example file:

# source, target, weight
0,1,1
0,2,2
0,3,2
0,4,1
0,5,1
0,6,1
1,18,1
1,3,1
1,4,2
2,0,1
2,25,1
#...

GraphML (.graphml, .xml)

Flexible format based on XML.

It can store hierarchical graphs, information (i.e., attributes or properties) about the graph, the nodes and the edges.

Main drawback: heavy disk usage (space, and I\O time)

Example of the file:

<?xml version="1.0" encoding="UTF-8"?>
<graphml xmlns="http://graphml.graphdrawing.org/xmlns"
         xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
         xsi:schemaLocation="http://graphml.graphdrawing.org/xmlns http://graphml.graphdrawing.org/xmlns/1.0/graphml.xsd">

  <!-- property keys -->
  <key id="key0" for="node" attr.name="_pos" attr.type="vector_float" />
  <key id="key1" for="graph" attr.name="citation" attr.type="string" />
  <key id="key2" for="graph" attr.name="description" attr.type="string" />
  <!-- [...] -->
  <key id="key8" for="edge" attr.name="weight" attr.type="short" />

  <graph id="G" edgedefault="directed" parse.nodeids="canonical" parse.edgeids="canonical" parse.order="nodesfirst">

   <!-- graph properties -->
   <data key="key1">[&apos;J. S. Coleman. &quot;Introduction to Mathematical Sociology.&quot; London Free Press Glencoe (1964), http://www.abebooks.com/Introduction-Mathematical-Sociology-COLEMAN-James-S/189127582/bd&apos;]</data>
   <data key="key2">A network of friendships among male students in a small high school in Illinois from 1958. An arc points from student i to student j if i named j as a friend, in either of two identical surveys (from Fall and Spring semesters). Edge weights are the number of surveys in which the friendship was named.</data>

   <!-- [...] -->

   <!-- vertices -->
    <node id="n0">
      <data key="key0">0.92308158331278289, 12.186082864409657</data>
    </node>
    <node id="n1">
      <data key="key0">1.2629064355495019, 12.213213242633238</data>
    </node>
    <node id="n2">
      <data key="key0">1.1082744694986855, 12.190211909578192</data>
    </node>

    <!-- [...] -->

    <!-- edges -->
    <edge id="e0" source="n0" target="n1">
      <data key="key8">1</data>
    </edge>
    <edge id="e1" source="n0" target="n2">
      <data key="key8">2</data>
    </edge>
    <edge id="e2" source="n0" target="n3">
      <data key="key8">2</data>
    </edge>
    <edge id="e3" source="n0" target="n4">
      <data key="key8">1</data>
    </edge>

    <!-- [...] -->

   </graph>
</graphml>

How to load a network

Choose a graph analysis library. The right one mostly depends on your needs (e.g., features, performance, etc.)
In this warm-up, we will use graph-tool.
To load the network, we need to use the right loader function, which depends on the file format
After identifying the file format and the right loader function, we load the network

g = gt.load_graph("highschool.graphml")

display(g)

<Graph object, directed, with 70 vertices and 366 edges, 1 internal vertex property, 1 internal edge property, 7 internal graph properties, at 0x7f1ed41879d0>

display(g.graph_properties)

{'citation': <GraphPropertyMap object with value type 'string', for Graph 0x7f1ed41879d0, at 0x7f1ed4187220>, 'description': <GraphPropertyMap object with value type 'string', for Graph 0x7f1ed41879d0, at 0x7f1ed4187130>, 'konect_meta': <GraphPropertyMap object with value type 'string', for Graph 0x7f1ed41879d0, at 0x7f1ed4187070>, 'konect_readme': <GraphPropertyMap object with value type 'string', for Graph 0x7f1ed41879d0, at 0x7f1ed41b80a0>, 'name': <GraphPropertyMap object with value type 'string', for Graph 0x7f1ed41879d0, at 0x7f1ed4225070>, 'tags': <GraphPropertyMap object with value type 'vector<string>', for Graph 0x7f1ed41879d0, at 0x7f1ed4225040>, 'url': <GraphPropertyMap object with value type 'string', for Graph 0x7f1ed41879d0, at 0x7f1ed4256d00>}

display(g.vertex_properties)

{'_pos': <VertexPropertyMap object with value type 'vector<double>', for Graph 0x7f1ed41879d0, at 0x7f1ed4187730>}

display(g.edge_properties)

{'weight': <EdgePropertyMap object with value type 'int16_t', for Graph 0x7f1ed41879d0, at 0x7f1ed4291130>}

Some network analysis

Get the number of nodes

number_of_nodes = g.num_vertices()
display(f"Number of nodes: {number_of_nodes}")

'Number of nodes: 70'

Get the number of edges

number_of_edges = g.num_edges()
display(f"Number of edges: {number_of_edges}")

'Number of edges: 366'

Get the in and out degrees

in_degree = g.get_in_degrees(g.get_vertices(), eweight=None)

average_in_degree = np.mean(in_degree)

display("Average in degree", average_in_degree)

'Average in degree'



5.228571428571429

out_degree = g.get_out_degrees(g.get_vertices(), eweight=None)

average_out_degree = np.mean(out_degree)
display("Average out degree", average_out_degree)

'Average out degree'



5.228571428571429

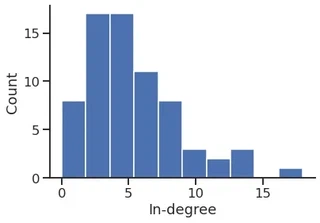
In-degree distribution

p = plt.hist(in_degree)
 
plt.ylabel("Count")
plt.xlabel("In-degree")
sns.despine()

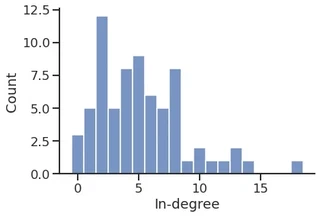
p = sns.histplot(in_degree,
                 stat="count",
                 discrete=True,
)
p.set_xlabel("In-degree")
sns.despine()

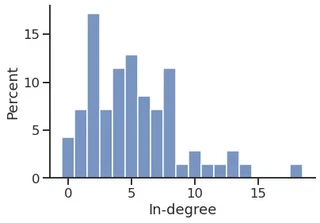
p = sns.histplot(in_degree,
             stat="percent",
             discrete=True,
)
p.set_xlabel("In-degree")
sns.despine()

sns.histplot(in_degree,
             stat="frequency",
             discrete=True,
)
plt.xlabel("In-degree")
sns.despine()

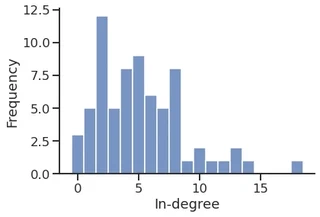
sns.histplot(in_degree,
             stat="percent",
             discrete=True,
             label="In-degree",
             legend=True,

)
sns.histplot(out_degree,
             stat="percent",
             discrete=True,
             label="Out-degree",
             legend=True,
)

plt.xlabel("Degree")
plt.legend()
sns.despine()

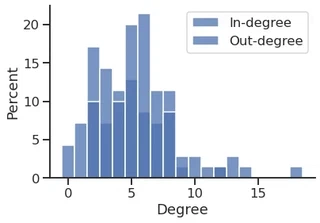
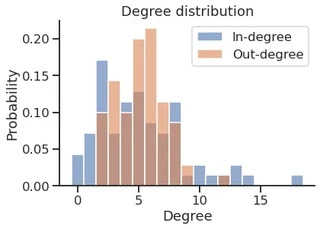
cmap = sns.color_palette("deep", n_colors=2)

cmap

sns.histplot(in_degree,
             stat="probability",
             discrete=True,
             label="In-degree",
             legend=True,
             color=cmap[0],
             alpha=0.6,
)
sns.histplot(out_degree,
             stat="probability",
             discrete=True,
             label="Out-degree",
             legend=True,
             color=cmap[1],
             alpha=0.6,
)

plt.title("Degree distribution")
plt.xlabel("Degree")
plt.legend()
sns.despine()

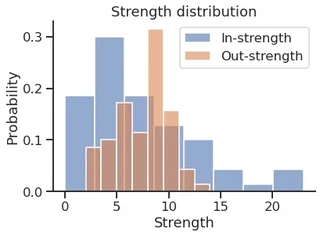
Get the in and out strength

weight = g.edge_properties["weight"]

in_strength = g.get_in_degrees(g.get_vertices(), eweight=weight)

out_strength = g.get_out_degrees(g.get_vertices(), eweight=weight)

sns.histplot(in_strength,
             stat="probability",
             discrete=False,
             label="In-strength",
             legend=True,
             color=cmap[0],
             alpha=0.6,
)

sns.histplot(out_strength,
             stat="probability",
             discrete=False,
             label="Out-strength",
             legend=True,
             color=cmap[1],
             alpha=0.6,
)

plt.title("Strength distribution")
plt.xlabel("Strength")
plt.legend()
sns.despine()

Store the values as a DataFrame

df = pd.DataFrame(
    data={
        ("Degree", "In"): in_degree,
        ("Degree", "Out"): out_degree,

        ("Strength", "In"): in_strength,
        ("Strength", "Out"): out_strength,
    },
)

df.head()

	Degree		Strength
	In	Out	In	Out
0	2	6	2	8
1	2	3	3	4
2	2	4	3	5
3	12	6	19	9
4	13	5	21	9

… and plot the DF using Seaborn

melted_df = pd.melt(df, var_name=["Kind", "Direction"], value_name="Value")

melted_df

	Kind	Direction	Value
0	Degree	In	2.0
1	Degree	In	2.0
2	Degree	In	2.0
3	Degree	In	12.0
4	Degree	In	13.0
...	...	...	...
275	Strength	Out	7.0
276	Strength	Out	10.0
277	Strength	Out	10.0
278	Strength	Out	4.0
279	Strength	Out	5.0

280 rows × 3 columns

facet = sns.displot(melted_df,
                    x="Value",
                    kind="hist",
                    row="Kind",
                    col="Direction",
                    hue="Direction",
                    )

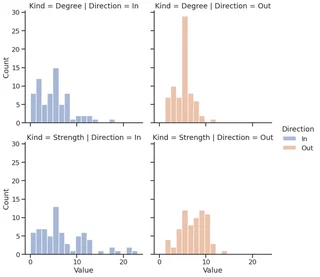
melted_df["Kind"] = melted_df["Kind"].apply(str.lower)

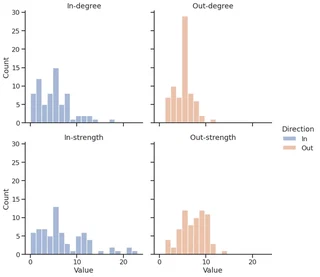
facet = sns.displot(melted_df,
                    x="Value",
                    kind="hist",
                    row="Kind",
                    col="Direction",
                    hue="Direction",
                    )

facet.set_titles(template="{col_name}-{row_name}")

<seaborn.axisgrid.FacetGrid at 0x7f1ecf5c6610>

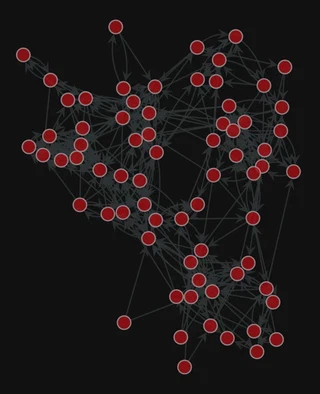
Graph visualization

1. Compute the node layout

pos = gt.fruchterman_reingold_layout(g, n_iter=1000)

2. Plot the network

gt.graph_draw(g, pos=pos,
              bg_color="#111",
              )

<VertexPropertyMap object with value type 'vector<double>', for Graph 0x7f1ed41879d0, at 0x7f1ed41312b0>

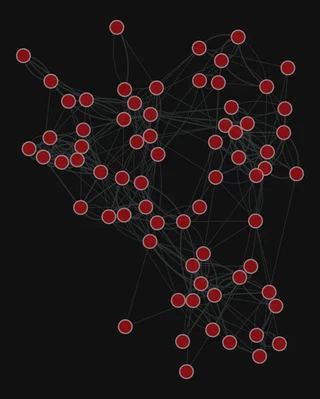
Add the edge weight

gt.graph_draw(g,
              pos=pos,
              edge_pen_width=g.edge_properties["weight"],
              bg_color="#111",
              )

<VertexPropertyMap object with value type 'vector<double>', for Graph 0x7f1ed41879d0, at 0x7f1ecf79e910>

More layouts

pos = gt.sfdp_layout(g)

gt.graph_draw(g, pos=pos,
              edge_pen_width=g.edge_properties["weight"],
              bg_color="#111",
              )

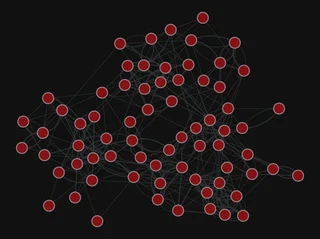
<VertexPropertyMap object with value type 'vector<double>', for Graph 0x7f1ed41879d0, at 0x7f1ecf79eca0>

pos = gt.arf_layout(g)

gt.graph_draw(g,
              pos=pos,
              bg_color="#111",
              )

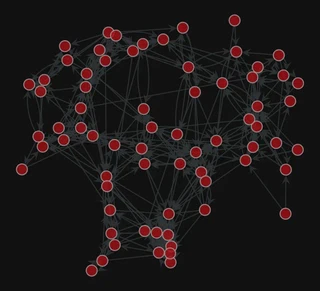
<VertexPropertyMap object with value type 'vector<double>', for Graph 0x7f1ed41879d0, at 0x7f1ed411b9a0>

pos = gt.random_layout(g)

gt.graph_draw(g,
              pos=pos,
              edge_pen_width=g.edge_properties["weight"],
              bg_color="#111",
              )

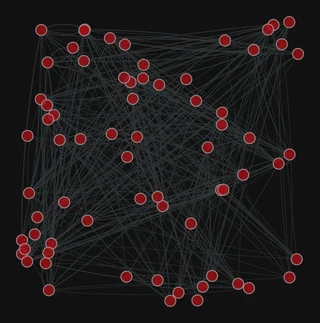
<VertexPropertyMap object with value type 'vector<double>', for Graph 0x7f1ed41879d0, at 0x7f1ecf645ac0>

Centrality computation

gw = gt.GraphView(g, vfilt=gt.label_largest_component(g))

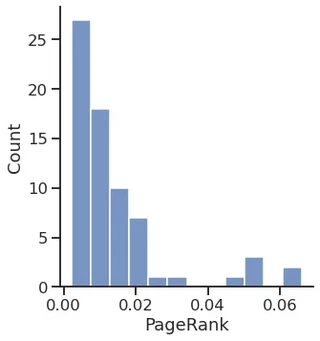
PageRank

pr = gt.pagerank(g)

sns.displot(pr.a)
plt.xlabel("PageRank")

Text(0.5, 15.439999999999998, 'PageRank')

Betweenness

vertex_betweenness, edge_betweenness =  gt.betweenness(g)

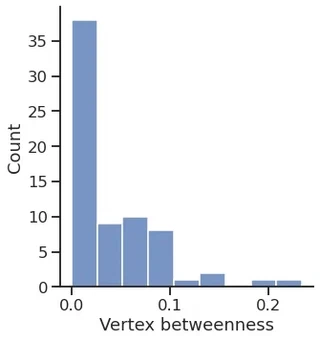
sns.displot(vertex_betweenness.a)
plt.xlabel("Vertex betweenness")

Text(0.5, 15.439999999999998, 'Vertex betweenness')

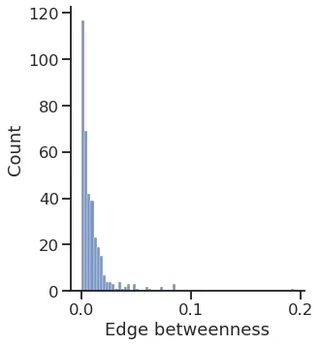
sns.displot(edge_betweenness.a)
plt.xlabel("Edge betweenness")

Text(0.5, 15.439999999999998, 'Edge betweenness')

gt.graph_draw(gw,
              pos=g.vp["_pos"],
              vertex_fill_color=pr, vorder=pr,
              edge_color=edge_betweenness,
              vertex_size=gt.prop_to_size(pr, mi=5, ma=15),
              vcmap=sns.color_palette("gist_heat", as_cmap=True),
              ecmap=sns.color_palette("rocket", as_cmap=True),
              edge_pen_width=g.edge_properties["weight"],
              bg_color="white",
              )

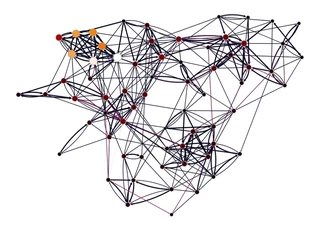
<VertexPropertyMap object with value type 'vector<double>', for Graph 0x7f1ed4113fa0, at 0x7f1ed40db340>

Inferring modular structure

# state = gt.minimize_blockmodel_dl(g)
state = gt.minimize_nested_blockmodel_dl(g)

state.draw()

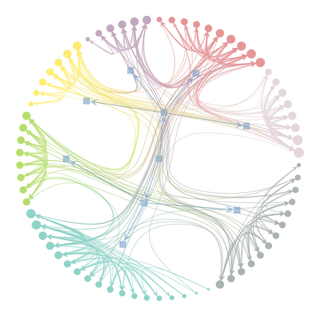
(<VertexPropertyMap object with value type 'vector<double>', for Graph 0x7f1ed41879d0, at 0x7f1ecf7d77c0>,
 <GraphView object, directed, with 80 vertices and 79 edges, edges filtered by (<EdgePropertyMap object with value type 'bool', for Graph 0x7f1ecf32dfa0, at 0x7f1ecf338040>, False), vertices filtered by (<VertexPropertyMap object with value type 'bool', for Graph 0x7f1ecf32dfa0, at 0x7f1ecf330ee0>, False), at 0x7f1ecf32dfa0>,
 <VertexPropertyMap object with value type 'vector<double>', for Graph 0x7f1ecf32dfa0, at 0x7f1ecf330eb0>)

levels = state.get_levels()

gt.graph_draw(g,
              pos=g.vp["_pos"],
              vertex_fill_color=levels[0].get_blocks(),
              edge_color=edge_betweenness,
              vertex_size=gt.prop_to_size(pr, mi=5, ma=15),
              vorder=pr,
              vcmap=sns.color_palette("tab10", as_cmap=True),
              ecmap=sns.color_palette("rocket", as_cmap=True),
              edge_pen_width=g.edge_properties["weight"],
              bg_color="white",
              )

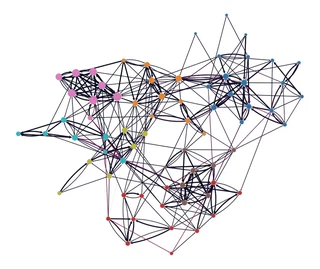
<VertexPropertyMap object with value type 'vector<double>', for Graph 0x7f1ed41879d0, at 0x7f1ecf3c9310>

Add some columns to our DataFrame

df["PageRank"] = pr.a

df["Betweenness"] = vertex_betweenness.a

df["Block"] = levels[0].get_blocks().a

df.head()

	Degree		Strength		PageRank	Betweenness	Block
	In	Out	In	Out
0	2	6	2	8	0.003871	0.024913	44
1	2	3	3	4	0.003502	0.002819	44
2	2	4	3	5	0.003602	0.005649	44
3	12	6	19	9	0.020530	0.081323	44
4	13	5	21	9	0.022862	0.079074	44

Save the DataFrame

To CSV (Comma Separated Values)

df.to_csv("dataframe.csv")

To Excel

df.to_excel("dataframe.xlsx")

PyTorch Geometric (PyG)

PyG is a library built upon PyTorch to easily write and train Graph Neural Networks (GNNs) for a wide range of applications related to structured data.

Library for Deep Learning on graphs

It provides a large collection of GNN and pooling layers

New layers can be created easily

It offers:

Support for Heterogeneous and Temporal graphs
Mini-batch loaders
Multi GPU-support
DataPipe support
Distributed graph learning via Quiver
A large number of common benchmark datasets
The GraphGym experiment manager

PyTorch Geometric documentation

Introduction by example

Each network is described by an instance of torch_geometric.data.Data, which includes:

data.x: node feature matrix, with shape [num_nodes, num_node_features]
data.edge_index: edge list in COO format, with shape [2, num_edges] and type torch.long
data.edge_attr: edge feature matrix, with shape [num_edges, num_edge_features]
data.y: target to train against (may have arbitrary shape)

import torch

from torch_geometric.data import Data

Let’s build our Data object

Node features

We do not have any node feature

We can use a constant for each node, e.g., $1$

x = torch.ones(size=(g.num_vertices(), 1),
               dtype=torch.float32
    )

display(x.shape)

display(x.T)

torch.Size([70, 1])



tensor([[1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
         1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
         1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
         1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]])

Connectivity matrix and edge attributes

edge_index = torch.empty(size=(2, g.num_edges()),
                         dtype=torch.long,
)

display("edge_index", edge_index.shape)

edge_attr = torch.empty(size=(g.num_edges(),),
                        dtype=torch.float32,
)
display("edge_attr", edge_attr.shape)

'edge_index'



torch.Size([2, 366])



'edge_attr'



torch.Size([366])

for i, (source, target, weight) in enumerate(g.iter_edges(eprops=[g.edge_properties["weight"]])):
    edge_index[0, i] = source
    edge_index[1, i] = target

    edge_attr[i] = weight


display("edge_index", edge_index[:, :10])

display("edge_attr", edge_attr[:10])

'edge_index'



tensor([[ 0,  0,  0,  0,  0,  0,  1,  1,  1,  2],
        [ 1,  2,  3,  4,  5,  6, 18,  3,  4,  0]])



'edge_attr'



tensor([1., 2., 2., 1., 1., 1., 1., 1., 2., 1.])

Create the Data instance

network_data = Data(
    x=x,
    edge_index=edge_index,
    edge_attr=edge_attr,
)

display(network_data)

Data(x=[70, 1], edge_index=[2, 366], edge_attr=[366])

Create the train and test set

For link prediction, we need positive (existent) and negative (non-existent) edges

We can use the RandomLinkSplit class, that does the negative sampling for us

from torch_geometric.transforms import RandomLinkSplit

transform = RandomLinkSplit(num_val=0,
                            num_test=0.2,
                            disjoint_train_ratio=0.2,
                            split_labels=False,
                            add_negative_train_samples=True,
                            neg_sampling_ratio=1.0,
                            is_undirected=False,
)
train_data, _, test_data = transform(network_data)

display(train_data)

Data(x=[70, 1], edge_index=[2, 235], edge_attr=[235], edge_label=[116], edge_label_index=[2, 116])

display(test_data)

Data(x=[70, 1], edge_index=[2, 293], edge_attr=[293], edge_label=[146], edge_label_index=[2, 146])

Create the model

Model architecture:

2x GINE convolutional layers
1x Multi-Layer Perceptron (MLP)

The GINE layers will compute the node embedding

We can build the edge embedding by, e.g., concatenating the source and target nodes’ embedding

The MLP will take the edge embeddings and return a probability for each

from torch_geometric.nn import MLP

class MLP(MLP):

    def __getitem__(self, item):
        return self.lins[item]

import torch.nn.functional as F
from torch_geometric.nn import GINEConv
from torch.nn import Sequential, Linear, ELU

class GINEModel(torch.nn.Module):
    def __init__(self, in_channels, hidden_channels, out_channels, edge_dim):
        super().__init__()
        self.conv1 = GINEConv(nn=MLP([in_channels, hidden_channels, hidden_channels]),
                             train_eps=False, edge_dim=edge_dim,) 

        self.conv2 = GINEConv(nn=MLP([hidden_channels, hidden_channels, out_channels]),
                             train_eps=False, edge_dim=edge_dim,)

        self.edge_regression = MLP(channel_list=[2 * out_channels, out_channels, 1],
                                   batch_norm=False, dropout=0.3)


    def forward(self, x, edge_index, target_edges):
        x = self.conv1(x=x, edge_index=edge_index, edge_attr=edge_attr)
        x = F.relu(x)
        x = self.conv2(x=x, edge_index=edge_index, edge_attr=edge_attr)
        x = F.relu(x)

        x = torch.hstack((
            x[target_edges[0, :]],
            x[target_edges[1, :]],
        ))
        x = self.edge_regression(x)
        
        return x

Let’s create the model instance

model = GINEModel(in_channels=network_data.x.shape[1],
                 hidden_channels=20,
                 out_channels=20,
                 edge_dim=network_data.edge_attr.shape[0],
)

display(model)

GINEModel(
  (conv1): GINEConv(nn=MLP(1, 20, 20))
  (conv2): GINEConv(nn=MLP(20, 20, 20))
  (edge_regression): MLP(40, 20, 1)
)

Create the optimizer and loss instances

optimizer = torch.optim.Adam(params=model.parameters(), lr=0.005, weight_decay=1e-4)
criterion = torch.nn.BCEWithLogitsLoss()
# criterion = torch.nn.MSELoss()

epoch = 0

Define the train function and train the model

def train():
    model.train()
    optimizer.zero_grad()

    edge_probability = model(train_data.x, train_data.edge_index, train_data.edge_label_index).squeeze()
    loss = criterion(edge_probability, train_data.edge_label)
    loss.backward()
    optimizer.step()
    
    return loss

Define the test function

@torch.no_grad()
def test():
    model.eval()

    edge_probability = model(test_data.x, test_data.edge_index, test_data.edge_label_index).squeeze()
    edge_probability = torch.sigmoid(edge_probability)    
    
    return edge_probability, test_data.edge_label

Training and testing

from tqdm import tqdm

for _ in tqdm(range(2001)):
    loss = train()

    if epoch % 500 == 0:
        display(f'Epoch: {epoch:03d}, Loss: {loss:.4f}')

    epoch += 1

 24%|███████████████████████████████████████████████████████████████████▏                                                                                                                                                                                                               | 489/2001 [00:02<00:05, 262.96it/s]


'Epoch: 2500, Loss: 0.0881'


 50%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏                                                                                                                                          | 991/2001 [00:04<00:04, 211.13it/s]


'Epoch: 3000, Loss: 0.1207'


 75%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▋                                                                     | 1495/2001 [00:06<00:01, 271.06it/s]


'Epoch: 3500, Loss: 0.0798'


 99%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████▏   | 1973/2001 [00:08<00:00, 291.01it/s]


'Epoch: 4000, Loss: 0.0769'


100%|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 2001/2001 [00:08<00:00, 241.67it/s]

edge_probability, test_y = test()

Evaluate the model performance

The torchmetrics package provides many performance metrics for various tasks

It is inspired by scikit-learn’s metrics subpackage

from torchmetrics import Accuracy, AUROC

accuracy = Accuracy(threshold=0.5)

auroc = AUROC()

display("Accuracy", accuracy(edge_probability, test_y.to(torch.int)).item())
display("AUROC", auroc(edge_probability, test_y.to(torch.int)).item())

'Accuracy'



0.6095890402793884



'AUROC'



0.6100582480430603

No results found

Warm-up: Network analysis with Python

Python

What is python

Why is python so popular?

Some real-world applications

How to get python?

Anaconda

Python virtual environments

Environment creation

Switch environment

Data analysis and visualization libraries

Network analysis and visualization libraries

NumPy

The ndarray

SciPy

Sparse matrices

Pandas

Supported file formas

DataFrame example

Series of the species

Unique species

Average bill length

Standard deviation of the bill length

Data filtering for male penguins

Average bill length for male penguins

Average bill length and weight for female penguins

Matplotlib

Some plot examples

Line plots

Scatterplots and histograms

Barplots

Simple barplot

Stacked barplot

Grouped barplot

Horizontal bar chart

(Nested) pie charts

Heatmaps

Violin and box plots

Stackplots

… and many more

Seaborn

Some more plot examples

Smooth kernel density with marginal histograms (source)

Joint and marginal histograms

Custom projections

Discovering structure in heatmap data

Bivariate plot with multiple elements

Network Analysis with Python

graph-tool

How to load a network

File formats

Edgelist (.el, .edge, …)

GraphML (.graphml, .xml)

How to load a network

Some network analysis

Get the number of nodes

Get the number of edges

Get the in and out degrees

In-degree distribution

Get the in and out strength

Store the values as a DataFrame

… and plot the DF using Seaborn

Graph visualization

1. Compute the node layout

2. Plot the network

Add the edge weight

More layouts

Centrality computation

PageRank

Betweenness

Inferring modular structure

Add some columns to our DataFrame

Save the DataFrame

To CSV (Comma Separated Values)

To Excel

PyTorch Geometric (PyG)

Introduction by example

Let’s build our Data object

Node features